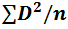Introduction
- Ram, Arjun, Ravi, Ashok are three friends of the same class and they are awaiting their exam results. All of them got 85% marks which were shocking as their response to the different papers were different, few had written English very well and few had written it bad. So how did this happen?
- Let us have a look at their scorecard of individual subjects which is out of 100:
| Subject/Student | English | Hindi | Maths | Science | Total percentage |
|---|---|---|---|---|---|
| Ram | 70 | 96 | 85 | 89 | 85 |
| Arjun | 99 | 45 | 99 | 97 | 85 |
| Ravi | 82 | 88 | 80 | 90 | 85 |
| Ashok | 60 | 82 | 99 | 99 | 85 |
- It is well known that the total percentage is the average percentage of each subject. Though the total percentage of all the four is the same, the scoring pattern of each of them is very different from each other.
- Hence, Average or Mean gives us detail about the overall picture only and it skips the individual contribution of all the elements.
- In other words, Average gives us information about the size or value of elements of the dataset (total percentage) and not about the spread of the values in elements i.e. how much or how less is the contribution of an element (percentage in each subject).
- The measure of dispersion helps us to overcome the drawback of the Mean observed above, it helps in understanding the contribution of each element in a dataset.
- Dispersion is a measure to find out the extent to which values on element differ from the Mean of dataset i.e. in the above example measure of dispersion will give us an idea that how much score did Ram got in each subject (how much or how less than 85).
- The population is the collection of specified groups of similar objects based on some common parameters. E.g. Residents of State of Maharashtra or All tigers in a Tiger Reserve
- The members of the population are known as Elements of the Population. e.g. Tiger is the element of a population that is defined as all tigers of the Tiger Reserve. The total number of elements in a Population is known as Population Size.
- There are various ways to measure the dispersion of a dataset which we will study in upcoming sections.
Population Standard Deviation
- Standard Deviation the most widely used method to measure the Dispersion of a set of data. It measures the deviation of elements of a population or dataset from its mean.
- Standard Deviation is calculated as the positive square root of the mean of squared deviations from the mean.
Example 1:
- Let us take a population: 2,5,8,10,12,15,18 and Calculate its Standard Deviation
- Solution:
- Step 1: Calculating Mean:
- Mean = (2+5+8+10+12+15+18)/7 = 70/7 = 10
- Step2: Calculating Deviation of Mean and its Square:
| Element | Deviation from Mean | D2 |
|---|---|---|
| 2 | -8 | 64 |
| 5 | -5 | 25 |
| 8 | -2 | 4 |
| 10 | 0 | 0 |
| 12 | 2 | 4 |
| 15 | 5 | 25 |
| 18 | 8 | 64 |
- Step 3: Calculating Mean of Square of Deviations:
- Mean of Square of Deviation = (64+25+4+0+4+25+64)/7 = 186/7 = 26.57
- Step 4: Taking Square Root of the Mean of Square of Deviations:
- Population Standard Deviation =
= 5.155
- A Generalised Formula for calculation of Population Standard Deviation can be:
- Population Standard Deviation =
- Where D is the difference between the elements of a population and its mean
- And n is the population size
- Standard Deviation depends on each value of the population, change in any of the values affects the Standard Deviation.
- Standard Deviation is easy to interpret, the rule of standard deviation says that almost all elements of a population should lie within Mean ± 3* Standard Deviation.
Population Variance
- Like standard deviation, Population Variance is a way to measure the dispersion of a population or a dataset. It is the square of the mean of squared deviations from the mean. It can also be obtained by squaring the Standard Deviation.
- To calculate Variance in a population the above steps must be followed up to step 3, the value obtained in step 3 will be the Variance of the dataset i.e. for the above population, the Variance is 26.57.
- A Generalised Formula for population Variance is,
- Population Variance =
- where D is the difference between the elements of a population and its mean
- And n is the population size